
 Dyfrakcja światła
Dyfrakcja światła
Podstawy teoretyczne dyfrakcji wynikają z zasady Huygensa (wymawiamy hojchensa), (czasem Huygensa-Fresnela, bo jej aktualną postać, w której fale elementarne sš spójne i uwzględnia się ich interferencję, podał A.J. Fresnel w XIX w.), sormułowana przez holenderskiego fizyka Christiaana Huygensa (1629 - 1695) pod koniec XVII w. Głosi ona, że każdy punkt powierzchni czołowej fali świetlnej jest źródłem wtórnych fal sferycznych, a postepujące w przestrzeni zaburzenie falowe jest wynikiem wzajemnego nakładania się fal. Funkcja opisująca drgania dla skalarnej fali sferycznych przyjmuje postać: F(x, y, z, t) = F(r, t). Ze wzoru można wyczytać, że na danej sferze o środku w punkcie, z którego fala się rozchodzi jest stała faza. Fale te zwane są falami cząstkowymi i interferują ze sobą. Ścisłe matematyczne uzasadnienie zasady Huygensa-Fresnela podał G. Kirchhoff. Zasadę stosuje się do wyjaśnienia zjawisk dyfrakcyjnych, czyli uginania się fal padających na przeszkody.
Jeśli na drodze równoległej wiązki światła znajduje się nieprzezroczysta przeszkoda P z otworem O, to na ekranie E, umieszczonym w pewnej odległości L od przeszkody P, obserwuje się pole świetlne o rozmytym brzegu i o średnicy większej od średnicy otworu O. Pole to jest tym wyraźniejsze, im mniejszy jest otwór O i im większa jest spójność wiązki śwtlnej. Na ekranie E oprócz rozmytego widoku pola otworu, występują prążki interferencyjne, zwane dyfrakcjami. Zasada Huygensa nie określa amplitudy fali. W ogólnym przypadku amplituda ta będzie zależała od geometrii układu i kierunku, w którym fala się porusza. W zależności od tego, jaka jest szerokość szczeliny O w porównaniu z długością fali, zjawisko dyfrakcji będzie mniej lub bardziej wyraźne. Są one wyraźnie zawsze wtedy, gdy O jest mniejsze od długości fali lub gdy O jest identyczne.
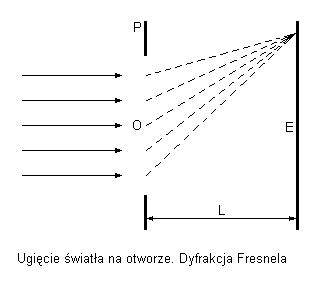
Ogólnie gdy fala płaska napotka na swej drodze przegrodę ze szczeliną, to czoło fali odbije się od przegrody, a punkt lub punkty szczeliny staną się źródłami fal kulistych. Fale te, nakładając się na siebie, utworzą falę wypadkową, której powierzchnia falowa ma inny kształt, niż miała fala przed dojściem do przeszkody. |
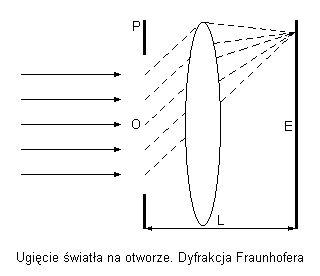
Zjawisko uginania się fali na przeszkodach, wynikające wprost z zasady Huygensa, nazywa się dyfrakcją. Rozróżnia się dwa rodzaje dyfrakcji: Fresnela i Fraunhofera, zwane również dyfrakcją w bliskim i dalekim polu. Pierwszą obserwuje się na ekranie, gdy odległość L jest niewielka, drugą gdy odległość L jest odpowiednio wielka, w szczególności nieskończona. Na poniższym rysunku jest przedstawiona dyfraskcja w dalekim polu, a soczewka została wstawiona w celu zmniejszenia potrzebnej odległości.
W teorii i praktyce holograficznej ważną rolę spełniają siatki dyfrakcyjne, które tworzą układy równych, równoległych i jednakowo rozmieszczonych szczelin utworzonych w przeszkodzie na drodze światła. Mówi się czasem o Stałej siatki dyfrakcyjnej, bo jest to jej charakterystyczny parametr. Wyraża on rozstaw szczelin siatki (odległość między środkami kolejnych szczelin). Każdy hologram można traktować jako mniej lub bardziej skomplikowaną siatkę dyfrakcyjną. Typowa siatka dyfrakcyjna ma 12000 szczelin na cal. Stała takiej siatki wynosi 2116 nm (d = 2,54 cm/12000). Najprostsza klasyczna siatka dyfrakcyjna składa się z periodycznie powtarzających się równoległych szczelin jak na rysunku.
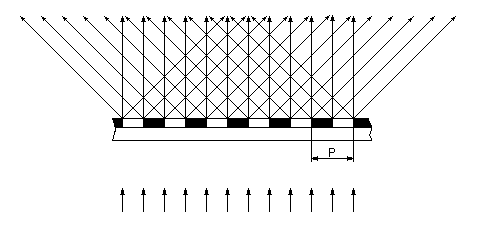
Taka siatka dyfrakcyjna po wstawieniu w bieg równoległej wiązki świetlnej siatka dyfrkakcyjna, powoduje ugięcie przechodzących przez nią promieni świetlnych pod różnymi kątami w przedziale 0° ÷ 90°. Wszystkie siatki dyfrakcyjne można podzielić na dwie główne kategorie: amplitudowe i fazowe.
W holografii mamy raczej do czynienia z siatkami dyfrakcyjnymi, których rozkład transmitancji jest bardziej lub mniej zbliżony do funkcji sin2x lub 1+sinx. Siatka, która przepuszcza amplitudę fali świetlnej według funkcji sin2x (lub cos2x) charakteryzuje się tym, że wytwarza tylko trzy maksima dyfrakcyjne: zerowe (S0) oraz plus (S+1) i minus (S-1) pierwszego rzędu.